Vous avez un projet d'épargne ?
Que ce soit pour défiscaliser, faire fructifier votre argent ou épargner pour vos enfants, notre simulateur vous guide vers les solutions adaptées à vos objectifs !
Les intérêts composés, c’est un peu comme des poupées russes : tes gains passés augmentent tes gains futurs.
Le principe ? Tes intérêts produisent à leur tour des intérêts avec le temps, un peu comme une boule de neige qui deviendrait de plus en plus grosse à mesure qu’elle dévale une pente !
Et c'est justement ce cercle vertueux qui donne aux intérêts composés leur fameux pouvoir d’enrichissement à long terme. Albert Einstein les appelait même... la “8e merveille du monde” ! Pour le physicien allemand, ce simple calcul applicable en investissement n’était pas reconnu à sa juste valeur.
Alors il est grand temps de se mettre à la page ! Et ça tombe bien, on te t'explique tout sur les intérêts composés dans cet article.
Et si on commençait par les intérêts ?
Pour comprendre les intérêts composés, il faut être au clair sur la définition des intérêts tout court.
Les intérêts bancaires
En deux mots, les intérêts, c’est le prix à payer pour emprunter de l’argent, c'est-à-dire la rémunération du prêteur. Quand tu fais un crédit bancaire, la somme que tu empruntes est appelée le capital. Tant que tu empruntes cette somme, tu dois en payer un pourcentage chaque mois, chaque trimestre ou chaque année selon le contrat. Ce pourcentage, c’est le taux d’intérêt, et la somme totale de ces paiements, tu l’as compris, ce sont les intérêts.
Le taux d’intérêt est calculé selon le type de contrat (crédit immobilier, crédit à la consommation, emprunt étudiant, etc.), la durée de l’emprunt, ou encore l’importance du capital emprunté.
Si tu veux aller plus loin, sache que les taux d’intérêt sont un outil économique majeur utilisé par les Etats et les banques centrales pour encourager la consommation des ménages ou jouer sur la valeur d’une monnaie par exemple.
Les intérêts en investissement
Quand tu investis en bourse, c’est un peu la situation inverse. C’est toi qui injectes ton argent dans l’économie et qui perçois des intérêts ! Si tu investis 1000 euros et que la somme totale de ton investissement à la fin de l’année vaut 1120 euros, ton capital investi est de 1000 euros et tes intérêts sont de 120 euros, soit 12 % de ton capital investi. Ce pourcentage annuel (ou mensuel, ou trimestriel), c’est le rendement de ton investissement.
La différence avec les intérêts que tu dois à ta banque, c’est qu’en investissement, ils ne sont pas déterminés à l’avance. Ils dépendent du type de produits sur lesquels tu investis, et plus particulièrement de leur performance.
Si tu investis sur des actions par exemple, c’est la performance de l’entreprise sur laquelle tu investis qui déterminera le prix de l’action et, in fine, ton rendement. Quant aux obligations, leur valeur dépend de la nature et de la capacité financière de l’institution qui l’a émise.
Seule exception à la règle : les livrets d’épargne, comme le livret A, qui eux, ont un taux d’intérêt fixé à l’avance, mais qui sont très faibles en contrepartie !
L’effet boule de neige des intérêts composés
Maintenant que le principe des intérêts n’a plus de secrets pour toi, rentrons dans le cœur du sujet : les intérêts composés !
Intérêts simples, intérêts composés ... kézaco ?
Imaginons que ton placement de 1000 euros a eu un rendement de 12 % cette année. Tu l’as compris, tes intérêts s’élèvent à 120 euros. 2 choix s’offrent alors à toi :
- Soit, tu récupères les 120 euros d’intérêts directement dans ta poche. On parle alors d’intérêts simples.
- Soit, tu décides de réinjecter tes 120 euros d’intérêts dans ton capital investi. Ton capital n’est donc plus de 1000 euros mais de 1120 euros pour la deuxième année. On parle maintenant d’intérêts composés.
L’intérêt de cette deuxième pratique, c’est qu’en supposant que tu aies un rendement positif chaque année, ton capital investi va gonfler chaque année, et donc tes intérêts aussi à rendement égal !
Si l'on cherchait à comparer le pouvoir des intérêts simples et ceux des intéreêts composés, concrètement, cela donnerait ça :
- Première situation : avec des intérêts simples, en récupérant tes gains chaque année, tu pourrais multiplier seulement par 3,5 ton capital de départ au bout de 20 ans.
- Deuxième situation : avec des intérêts composés, en réinjectant tes gains annuels dans ton capital investi, tu pourrais multiplier par 10 ton investissement de départ au bout de 20 ans.
Le choix est vite fait, non ?
La logique à long terme des intérêts composés
Ce qui est particulièrement intéressant avec les intérêts composés, c’est qu’ils font grossir le capital tout en y étant proportionnel, il s’agit donc d’un cercle vertueux dont les effets sont exponentiels !
En bref, les gains que t’apportent les intérêts composés sont de plus en plus important, et ce de plus en plus vite. Ils peuvent donc être quasiment négligeables les premières années, mais faire doubler tes gains quelques années plus tard. C’est pour ça qu’il faut les considérer sur le long terme, et que ne pas s’y intéresser sous prétexte qu’ils ne font pas de grandes différences sur 2 ou 3 ans, c'est dommage !
C’est en partie grâce à cet effet boule de neige, trop souvent oublié, que Warren Buffett est devenu milliardaire.
Pour aller plus loin, tu peux faire le calcul avec tes propres variables !
Calcul de ta somme finale avec intérêts simples :
Cn = Co*(1 + i*n)
Calcul de ta somme finale avec intérêts composés :
Cn = Co*(1 + i)^n
Où Co = ton capital de départ, n = le nombre d’années d’investissement, Cn = le capital au terme des n années, et i = ton rendement annuel (en supposant qu’il soit constant, tu peux faire une moyenne)
Quelques exemples d’application
Comme il n’est pas toujours évident de visualiser la puissance des intérêts composés de tête, voici quelques exemples qui devraient te donner une idée concrète de ce qu’ils peuvent changer dans ta stratégie d’investissement !
Exemple 1 : comparons intérêts composés et intérêts simples
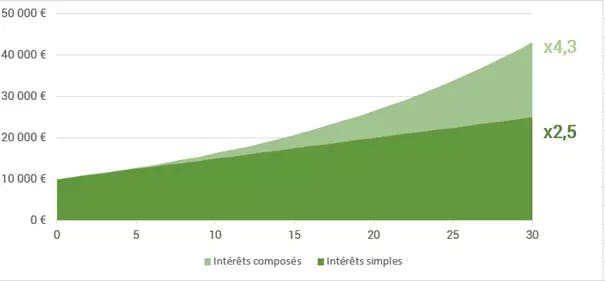
Imaginons un placement de 10 000 € sur 30 ans, avec un rendement de 5 % par an. Le capital et les intérêts seront de 25 000 € au bout des 30 ans si on applique les intérêts simples, contre 43 220 € en appliquant les intérêts composés. Soit 33 220 € d’intérêts totaux, contre 15 000 € sans réinvestir ses intérêts, plus du double !
On peut également observer que la somme totale grandit à vitesse constante dans le premier cas, alors qu’elle croit de plus en plus vite avec les intérêts composés.
Exemple 2 : comparons 2 stratégies
Voilà un exemple encore plus flagrant qui montre l’intérêt d’investir tôt et régulièrement. Un investisseur qui place 2 000 € par an pendant 30 ans sur un placement à 5 % aura une somme supérieure à un investisseur qui investit 10 000 € par an pendant 10 ans. A savoir 139 522 € contre 132 068 €. Pourtant, le second investisseur a investi 40 000 € de plus… Le temps donne bien souvent plus de résultats que la mise de départ !
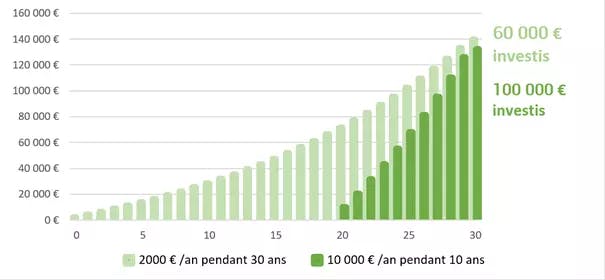
C’est pour ça qu’on te conseille d’investir le plus tôt possible, même des petites sommes. Car en investissement, ton meilleur allié est le temps !
Si tu veux commencer à investir, mais que tu as peur de ne pas avoir le temps ou la connaissance nécessaire, Mon Petit Placement peut t’aider à sauter le pas !
Définis en quelques minutes ton profil d’investisseur avant de recevoir un conseil sur-mesure. Pour investir petit à petit, tu peux également mettre en place un virement automatique régulier de ton capital investi. Consulte notre simulateur pour savoir combien tu pourrais gagner !






